二次剩餘（Quadratic Residue）與二次非剩餘（Quadratic Nonresidue）

• 如果存在一個整數x使 x² ≡ a (mod p)，則a為mod p的 二次剩餘
• 若這樣的x不存在，則a為 二次非剩餘
• 如果p是一個奇質數，則在{1,2,…,p−1}中，mod p的二次剩餘數量與二次非剩餘數量均為(p-1)/2
• 若a是二次剩餘，則存在兩個解 x 和 -x，除非 x ≡ 0

回到題目

Quadratic Residues

https://cryptohack.org/courses/modular/root0/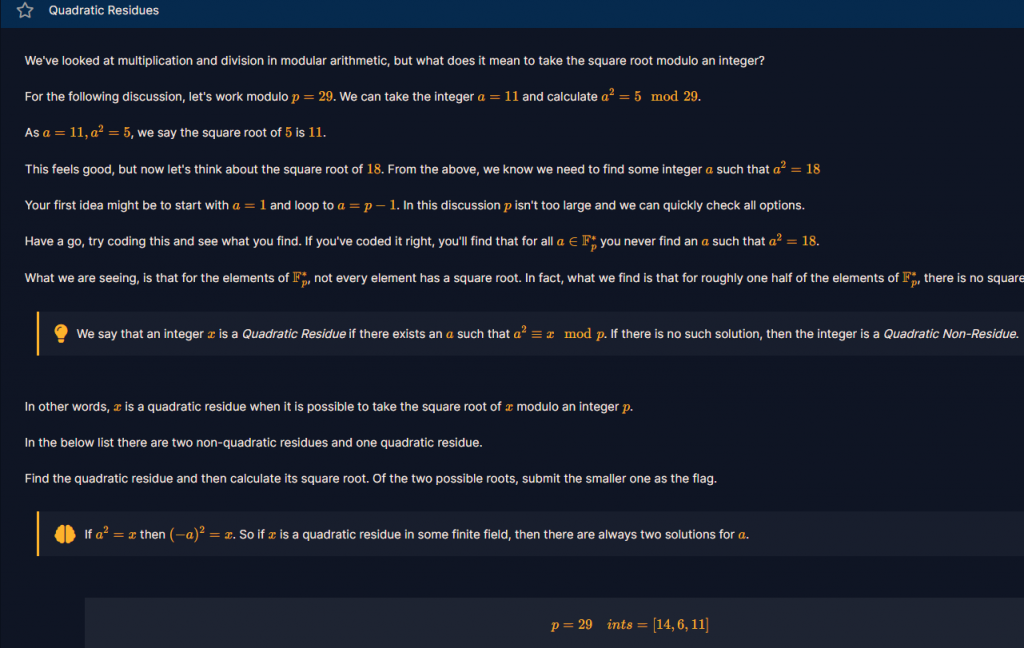

題意:

介紹了模運算中的二次剩餘（Quadratic Residue）的概念。
題目要我們再給定的數 p=29, ints=[14,6,11] 中，找出 mod p 的二次剩餘，而其平方根（取較小的）就是答案。

解題過程:

###找出ints中的二次剩餘x，並求出a
#a² ≡ x (mod p)
p=29
ints=[14,6,11]
# 遍歷從 1 到 p-1 的所有整數
for i in range(1,p):
    if((i*i)%p==14):
        print(f"quadratic residue is 14, root={i}")
    if((i*i)%p==6):
        print(f"quadratic residue is 6, root={i}")
    if((i*i)%p==11):
        print(f"quadratic residue is 11, root={i}")

print 出:
quadratic residue is 6, root=8
quadratic residue is 6, root=21
最後得到二次剩餘為6，此時的平方根分別是8和21，題目要求我們返回較小的數值，所以答案就是8。

8

參考資料

wiki: https://zh.wikipedia.org/zh-tw/%E4%BA%8C%E6%AC%A1%E5%89%A9%E4%BD%99
前人的文章: https://ithelp.ithome.com.tw/m/articles/10323070
oi-wiki: https://oi-wiki.org/math/number-theory/quad-residue/

後話

今天的內容比較少，明天之後應該就比較能空出時間來寫了，明天會寫歐拉準則和勒讓得符號。